by Craig

Password difficult to remember and easy to break?

linkedin lottery passwords

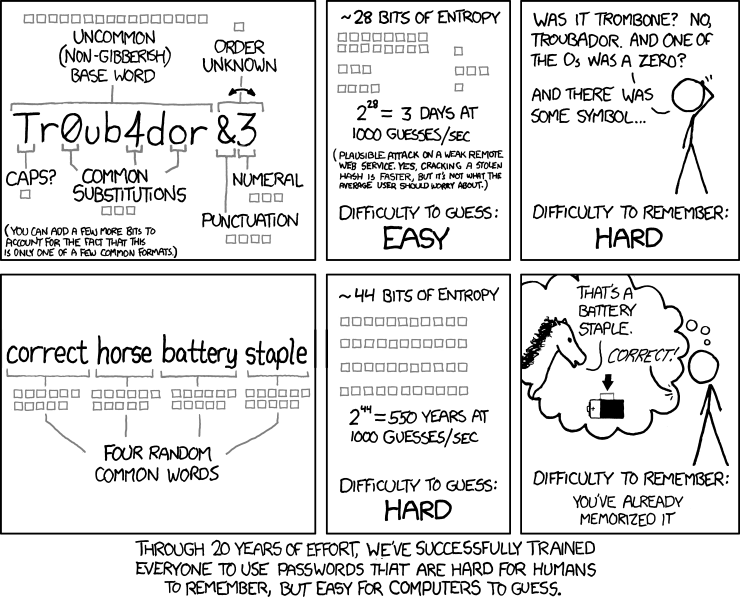
It may just be a comic but there is a huge amount of truth in it (from www.xkcd.com): Password Strength

So what is the above above then?

Well it’s the same trick that the lottery uses to get you to buy tickets on games with impossibly high odds such as Euromillions - any extra digit hugely increases the difficulty/probability of the guess.

Take a normal password, so “pass”, and try and guess it. That’s 4 digits long so you need to guess the right combination out of the 26 letters of the alphabet - 1/26 x 1/26 x 1/26 x 1/26 which is 1/456,976 or 1 in 456,976 probability of a correct guess.

So lets capitalise letters (“pAss”) and say the case has to be correct as well. That gives us 2 chances per letter or 1/52 per digit and equates to (1/52 x 1/52 x 1/52 x 1/52 = 1/7,311,616)  1 in 7,311,616 probability.

If we go back to the “not caring about uppercase/lowercase” earlier example and add 1 more digit to the password to become “passe” then our password guess probability becomes: (1/26 x 1/26 x 1/26 x 1/26 x 1/26) 1 in 11,881,376 which is much, much more than our introduction of a capital letter (1 in 7,311,616).

The general principle, therefore, is that the longer the password the harder it is to guess no matter whether you use case sensitivity or numbers or punctuation. The only exception to this is where you use a real word, like “passe”, instead of a made up one, like “passm”, as a dictionary attack would circumvent the guessing.

The example above uses 1000 guess from a random computer attack a second. Using our passwords above the following would be the time taken to guess them:

  • “pass” - 1:456,976 - guessed in 7 to 8 minutes
  • “pAss” - 1 in 7,311,616 - guessed in just over 2 hours
  • “passe” - 1 in 11,881,376 - guessed in just over 3 hours

So there you go, longer words are much better than one with a few letters changed in it and even better if they have number substitutions as well!

Lotteries (incidentally)

The Euromillions is ridiculously difficult to win because of the extra digits you need to guess under the same principle. Here follows the maths:

Normal UK Lottery - 6 numbers guessed all between 1 and 49 so the probability calculation is:

6/49 x 5/48 x 4/47 x 3/46 x 2/45 x 1/44 =  720/10,068,347,520 or 1 in 13,983,816 (which is alot!)

For Euromillions it is 5 numbers guessed all between 1 and 50 and then 2 more between 1 and 11. This seems better right? It’s not because you have to guess 7 numbers in total and that makes all the difference:

5/50 x 4/49 x 3/48 x 2/47 x 1/46 x 2/11 x 1/10 = 240/27967632000 or 1 in 116,531,800 (which is loads!)

If we just strip out one of the end guesses (so drop the 2/11 and make it a single 1/10) then the odds drop to 1 in 21,187,600 and all because we only had to guess one number between 1 and 11 rather than 2….

Conclusion?

Yes i am sure there was one! Practice what you preach; I for one use normal everyday words in my passwords and put a # symbol between them so; “coffee#please” would be a very good password!